It's been a few months ago that I wrote a series of blog posts about Solon Voting. Solon is a project I started in July to implement cryptographically secure e-voting for direct democracy platforms, in particular Liquid Feedback which is used by the Pirate Party and other organizations in Central Europe. In the previous posts I already covered how delegated voting works, and how to divert the data flow of Liquid Feedback so that the voting phase could be handled by a cryptographically secure e-voting module. In the last post I then went on to look at requirements for secure e-voting. Those requirements are frequently referenced in this post.
Having laid out the requirements, I want to spend this post on briefly talking about the algorithms that exist for cryptographically secure e-voting. This is very superficial of course, it's intended to be layman understandable for those that don't really want to read the highly mathematical academic papers on the topic. If you do want to read academic papers, you can find lots of them on Google Scholar, just search for "e-voting" and you're all set for months to come! (No, I'm not qualified to recommend you any good papers. Just go and Google for something just like I did and if you find something interesting, let me know!)
While remaining high-level, I will mention several cryptographic building blocks such as mix-nets, blind signatures, zero knowledge proofs, and so on... and I won't bother explaining all of them. Your next step would be to look them up on Wikipedia, and then again Google Scholar.
The high level story is actually quite simple. There are plenty of e-voting protocols proposed, but I've found that most of them are variations on 2 different categories. I'll explain both of them in this post. The latter is the one I'm interested in for Solon.
Mixnet based e-voting
The first e-voting algorithms (that I know of) were proposed in the late 80's. I've come to call them "mix-net based" as the privacy requirement is implemented by a mix-net. I've previously referenced the paper A framework and taxonomy for comparison of electronic voting schemes by K Sampigethaya, R Poovendran, Computers & Security, Elsevier 2006. It seems this paper uses the categorization "Hidden voter".
The mixnet based approach is easy to understand because the sequence of cryptographic building blocks closely resembles how a classic paper based voting occurs too:
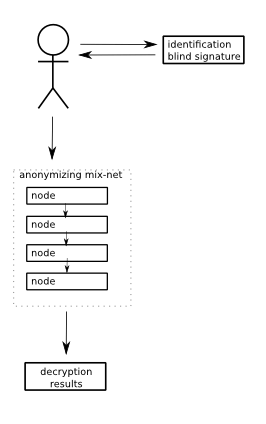
- The voter prepares the plaintext ballot and encrypts it so that only he himself is able to decrypt it. He also calculates so called zero-knowledge proofs to assure that the encrypted vote is in fact a valid vote. (For example, the vote cannot embed some identifying information about the voter, so as to become a receipt.)
- The voter then authenticates himself with the Voting Authority, who checks that the voter is eligible to vote. He also checks the zero-knowledge proofs to verify that the encrypted message in fact includes a valid vote and nothing else. If so, the voting authority will apply a blind signature to the encrypted vote (see below what that means). Finally, the authority will record that the voter has voted, so that he can vote only once.
- The voter receives the signed vote back and decrypts it. He now holds a plaintext ballot which is signed by the voting authority. This is what blind signature means: the voting authority is able to sign the plaintext contents of the vote, even if it is encrypted. Now the encryption is removed, but the plaintext is still signed. At the end of voting, only properly signed ballots will be counted.
- The voter now encrypts the vote with the public key used for the elections. He then sends the vote through an anonymizing mix-net. This would be a network of independently operated computers, each of which will somehow shuffle the incoming votes and then send them in a different order to the next node in the mix-net. Each link in the mix-net could also include its own encryption-decryption, on top of the encryption the voter already applied to the plaintext vote. The point of all this is to anonymize the votes - nobody should be able to track which vote was originally cast by which voter.
- When voting has closed, all votes are decrypted. To ensure that nobody can decrypt any votes ahead of time (fairness) you would typically use some threshold public key cryptography.
- Plaintext votes are counted.
Note how the above steps correspond to the steps you would take in a classic election:
- Go into the booth and write down the number or check the box of the candidate you are voting for, then fold your ballot.
- Show your ID to the voting clerks, who will then stamp your ballot.
- (This step has no counterpart in classic elections.)
- The vote is dropped into the ballot box. The votes are shuffled in the box and thus anonymized.
- Ballot box is opened.
- Votes are counted.
At this point you should already see some potential weaknesses in the above scheme. How do we know that the nodes in the mix-net don't cheat? They could for example drop some votes and don't forward them. Ok, since we know the total amount of votes cast, the voting authority would see that some votes are missing. Otoh, maybe the corrupt nodes could then also duplicate the same amount of votes to make the total match. Still, what if there are votes missing? Who would we blame?
Most of these questions are solved with using mix-net algorithms that are verifiable. The nodes in the mix-net are required to publish some mathematical proofs that verify that they forwarded all messages correctly, without of course revealing how exactly they shuffled the messages. Such proofs make the process more verifiable.
Still, some robustness issues remain in these schemes. What if the voting authority has signed a vote and returns it to the voter, but the voter never submits the vote to the first node in the anonymizing mix-net? This could happen for example due to a power failure. There doesn't seem to be any way to allow the voting authority to sign a new vote from the same voter - his vote is simply lost forever. Also the voter could have his vote signed and on purpose never submit it to the mix-net (or the first node could reject some votes and we would never know which of them to blame). Now the total amount of votes signed again would not match the total amount of votes actually counted.
A good property of this scheme is that it doesn't really put any restrictions on the contents of the ballot. You could encrypt pretty much anything, like a complex XML document, if there is a need for it.
Fun fact: Several of the building blocks in the above scheme are used also for other purposes. For example, Tor (The Onion Router) is a kind of mix-net. Digicash, an early form of digital and anonymous money transfers, was also based on blind signatures (I don't know if Bitcoin is?).
Homomorphic e-voting algorithms
So called homomorphic encryption algorithms have an interesting property: If you multiply the encrypted messages and then take the result and decrypt it, you will get the same result as if you would first decrypt all messages and then sum them together. It turns out such a property is very useful in an e-voting algorithm...
An e-voting algorithm based on homomorphic encryption would then work as follows:
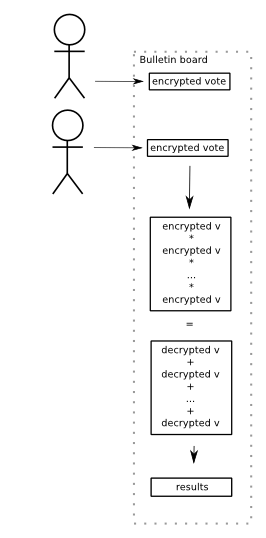
- The voter prepares a plaintext ballot and encrypts it with a homomorphic encryption algorithm. He also provides zero-knowledge proofs that the contents of the encrypted ballot is a valid ballot. He also signs the ballot, identifying himself. Only one vote, which must be properly signed, from each voter is counted in the end.
- The encrypted vote, the proofs and the signature are all posted on a public, non-erasable bulletin board. Academic articles typically don't bother with the details of how to actually implement such a device, but in practice this would again have to be implemented with some kind of distributed trust scheme. Imagine a cluster of servers operated by independent parties, exposing only an "INSERT" operation and nothing else. Anyway, notice the novelty of this approach: Instead of sending your votes into some anonymizing ballot box, all votes are posted in public for everyone to see. At least the verifiability of this approach seems to be well taken care of!
- After voting has closed, the voting authorities will multiply all votes with each other. Again this happens in public, and of course anyone could do the same multiplication.
- The voting authority then take the result of the multiplication and decrypt that. Individual votes are never decrypted. (Again you would have to use a threshold public key decryption scheme to ensure that.)
- Anyone can see the result. Anyone can also verify that the result is the plaintext of the encrypted result. (How exactly depends on the encryption algorithm used, but trivially this could be just by re-encrypting the plaintext and comparing the results.)
If you understood any of the above, you should be able to appreciate how this approach excels at least in the universal verifiability and robustness aspects. There's no mixing and shuffling and hidden channels going on, rather everything happens in public, but without compromising the privacy of an individual voter.
The main drawback in these schemes is that the algorithm will restrict the format of the plaintext ballot. Typically it can only be a number, or some kind of a bitmap. This of course makes sense, if you're going to blindly multiply the ballots together, they can't contain arbitrary content like text or xml or json. This constraint will haunt us in trying to use this kind of algorithms for the kind of ballots used in LiquidFeedback. I will write about how I plan to accomplish that integration in my next blog post about Solon.
The first homomorphic protocols that I've read about are from late 90's by scholars like Gennaro, Kramer, Schoenmakers, Franklin and Yung. The first of them was very simple, it only allowed a single-bit YES/NO vote. Future work has extended from there. In previous posts I've referenced a 2004 paper by Alessandro Acquisti that is already quite a mature approach.
After writing about Solon in 2012 a couple of people pointed me to an open source project from 2008 called Helios Voting. As it happens, this software also implements a simple variant of the homomorphic e-voting approach. There's a lot of useful stuff implemented there, for example the do the client side computation inside the browser, using a combination of JavaScript and Java.
In terms of practical usability, Helios have made some interesting design decisions that I think make sense. For example, they have skipped the requirements to implement some complicated distributed cluster and just gone for a single server approach for now. This means that a corrupt sysadmin could in fact decrypt individual votes (privacy), decrypt results ahead of time (fairness) or simply shut down his server or reject individual votes (robustness). Still, the one thing the sysadmin could not do is to forge the result of the voting, because everything needed for universal verifiability is still there.
Helios is implemented in Python and PostgreSQL, and the client side bits are browser based HTML, JavaScript and JavaScript calls into Java. For Solon this means that the goal is now to use Helios as a secure e-voting module, replacing the dummy backend that is in solon-voting 0.1. This would essentially make Solon an integration layer that transfers data between Liquid Feedback and Helios Voting. Cryptographically secure direct/delegated democracy is only one step away now!
Ben Adida, the creator of Helios Voting, recently made a public lecture on Air Mozilla about voting and e-voting. Towards the end he spends some 10 minutes explaining the homomorphic e-voting approach. I warmly recommend this lecture if this topic is interesting to you.
And you wouldn't have read this far if that weren't the case!
- Log in to post comments
- 31285 views

Another approach
Just found this page when looking for voting algorithm discussions. Here is another distributed approach to e-voting, that takes both anonymity into account, as well as security:
https://docs.google.com/document/d/1SPYFAkVNjqDP4HOt_A_YGFZy-SFXVxHoN1h…